이번에는 스레드 이진 트리에 대해 공부해 보자.
보통 이진 트리를 순회할 때 순환 호출을 사용한다. 만약 이진 트리의 노드 개수가 많아지고 트리의 높이가 높아진다면 순환 호출은 상당히 비효율적이다. 그럼 순환 호출을 사용하지 않고 구현할 수 있는 다른 방법이 무엇일까?

먼저 위 이진 트리를 보자.
| 노드 개수 | 7개 (N) |
| 총 링크의 개수(노드당 링크 2개) | 14개 (2N) |
| 다른 노드를 가리키는 링크의 수 | 6개 (N-1) |
| NULL을 가리키는 링크의 수 | 8개 (N+1) |
표와 같은 규칙을 가진다. NULL을 가리키는 링크는 N+1개나 존재하지만 사용하지 않는다. 스레드 이진 트리의 가장 큰 아이디어는 NULL을 가리키는 링크를 이용해 순환 호출 없이 트리의 노드들을 순회할 수 있도록 하는 것이다. NULL 링크에 중위 순회 시에 후속 노드인 중위 후속자를 저장시켜 놓아 순회 시 NULL을 가리키는 링크로 가더라도 순회가 계속 되도록 한다. 스레드 이진 트리(Thread Binary Tree)라는 말과 같이 실(Thread)을 이용해 순회 순서대로 연결시켜 놓은 트리인 것이다. 이 말은 직접 코드를 구현해 본다면 느낌이 올 것이다.
그럼 C언어로 직접 구현해 보자.
##함수
1. 트리노드의 구조체 선언
-> 트리노드의 기본적인 형태와 스레드 값을 저장해 줄 태그 필드 추가 선언
2. find_successor()
-> 후속자를 반환하는 함수
3. inorder_thread()
-> 중위 순회를 하는 함수
1) 트리노드의 구조체 선언
typedef struct TreeNode{
int data;
struct TreeNode *left,*right;
int thread; // 스레드이면 1, 스레드가 아니면 0
}TreeNode;스레드 이진 트리에서는 NULL을 가리키는 링크가 NULL을 가리키거나, 다른 노드를 가리키는, 2가지 경우가 있다.
그 2가지 경우를 구별해 주는 태그 필드가 추가되었다. 만약 thread 값이 1이라면 오른쪽 자식 노드가 중위 후속자가 되고, 값이 0이라면 그냥 오른쪽 자식을 가리키는 포인터가 된다.
2) find_successor()
TreeNode* find_successor(TreeNode *p)
{
TreeNode *q=p->right; // q는 p의 오른쪽 포인터
if(q==NULL || p->thread == 1) // q가 NULL이거나 스레드가 1이라면 q를 반환
return q;
while(q->left != NULL) // 왼쪽이 NULL이 아닌경우(오른쪽 자식인경우)
q=q->left; // 가장 왼쪽으로 이동
return q; // if문 while문 어느 조건에도 걸리지 않을경우 그냥 q반환
}q는 p의 오른쪽 노드로 q가 NULL 이거나 스레드가 1인 경우 while 문 이전에 q를 반환한다. q가 NULL인 경우는 단말 노드인 경우이며, 스레드가 1인 경우는 오른쪽 링크가 후속자 노드로 향하는 경우이다. 이때 후속자 노드로 부모 노드 혹은 상위 노드로 향하는 경우가 많기 때문에 if 문이 존재하지 않는다면 while 문의 (q->left !=NULL) 조건에 걸릴 가능성이 다분하다. 그렇기에 if 문을 while 문 이전에 조건을 추가하여 선언해 줘야 한다.
3) inorder_thread()
void inorder_thread(TreeNode *t)
{
TreeNode *q=t; // 트리 복사
while(q->left) q=q->left; // 가장 왼쪽으로 이동
do{
printf("%c -> ",q->data); // 처음 노드 출력한 뒤 후속자 노드 반환
q=find_successor(q); // 후속자 함수 호출
}while(q); // q가 NULL이 될 때까지 반복
}반복문을 시작하기 전에 가장 왼쪽 노드로 먼저 이동해놓고 시작한다. do-while 반복 문의 특성으로 먼저 1번은 실행하므로, 가장 왼쪽 노드를 처음 출력되고 계속 반환된 후속자를 출력하며 q가 NULL이 될 때까지 반복된다.
코드를 전체적으로 구현해 보자.
TreeNode b1 = {'A',NULL,NULL,1};
TreeNode b2 = {'B', NULL, NULL,1};
TreeNode b3 = {'C',&b1,&b2,0};
TreeNode b4 = {'D',NULL,NULL,1};
TreeNode b5 = {'E', NULL, NULL,0};
TreeNode b6 = {'F', &b4, &b5,0};
TreeNode b7 = {'G',&b3,&b6,0};
TreeNode *ThreadTree = &b7;
int main()
{
// 스레드 설정 -> 스레드는 입력해주는 값
b1.right = &b3; // A->right=&C
b2.right = &b7; // B->right=&G
b4.right = &b6; // D->right=&F
// 중위순회
inorder_thread(ThreadTree);
printf("\n");
return 0;
}임의로 생성한 스레드 이진 트리이다. 그림으로 보자면 이렇다.
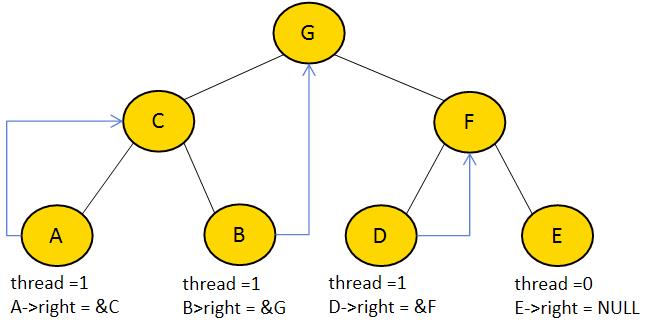
반복문 안에서 어떻게 실행되나 하나하나 따라가 보겠다.
| 삽입 q | q=p->right | 조건 | return q |
| q=A | A->right = C | thread ==1 | C |
| q=C | C->right = B | if문, while문 조건에 안걸림 | B |
| q=B | B->right=G | thread==1 | G |
| q=G | G->right=F |
q->left != NULL
(while 문) |
D |
| q=D | D->right = F | thread ==1 | F |
| q=F | F->right = E | if문, while문 조건에 안걸림 | E |
| q=E | E->right=NULL | q==NULL | NULL |
NULL을 반환한 것으로 while 문은 종료된다. 메인문을 실행시켜보면 다음과 같은 결과가 나온다.

중위 순회의 결괏값과 같음을 확인할 수 있다. 지금까지 구현해 본 스레드 이진 트리는 정말 간단한 형태의 스레드 이진 트리이다. 스레드 이진트리는 순회를 빠르게 할 수 있다는 장점도 있지만 스레드를 설정하기 위해 삽입이나 삭제 함수가 더 많은 일을 해야 하는 단점도 있다. 스레드 이진 트리의 간단한 예를 통해 스레드 이진 트리의 전체적인 흐름을 조금이나마 쉽게 이해할 수 있을 것이다.
'SW > Data structure' 카테고리의 다른 글
| (C언어) 연결 리스트(2)(삽입, 삭제 연산) [자료구조] (0) | 2022.03.29 |
|---|---|
| (C언어) 연결 리스트(1)(노드의 정의,생성,연결) [자료구조] (0) | 2022.03.05 |
| (C언어) 연결 리스트로 스택 구현해 보기[자료구조] (0) | 2022.02.19 |
| [자료구조] 리스트(List) (0) | 2022.02.19 |
| (C언어)연결 리스트로 큐 구현해 보기[자료구조] (0) | 2022.02.09 |
