2진법과 8진법, 10진법, 16진법의 의미를 알아보고 각 진법 간의 변환하는 방법을 알아보자.
컴퓨터는 정보를 표현하기 위해 비트라는 기본단위를 사용한다. 비트(bit)는 Binary Digit의 줄임 말로 2가지 상태( 0 or 1) 로만 표현 가능하다. 1비트는 $2^1$개, 2비트는 $2^1$개, n비트는 $2^n$개의 숫자를 표현할 수 있다. 이렇게 0과 1을 이용해 무한개의 숫자를 표현하는 방법이 2진법이다. 그보다 많은 수인 0부터 9까지의 숫자를 이용하여 표현하는 방법은 10진법 ,같은원리로 8진법, 16진법이 있다. 먼저 10진법으로 표현한 숫자를 보자.
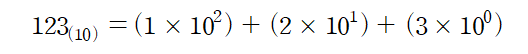
각 자릿수가 가지는 의미는 무엇일까?? 2진법으로의 변환원리를 알기 위해서 이렇게 해석해보려 한다.
숫자 3은 10으로 1번 나누었을 때의 나머지이다.
숫자 2는 10으로 2번 나누었을 때의 나머지이다.
숫자 1은 10으로 3번 나누었을 때의 나머지이다.
이 해석을 잘 기억하고 10진법을 2진법으로 바꿔보자.
10진법을 2진법으로 변환하기 위해 2진수의 자릿수를 먼저 살펴보자.

10진법을 2진법으로 바꾸기 위해서는 2진법의 정수부분과 소수 부분을 나눠서 봐야 한다. 먼저 정수 부분부터 보자.
#정수 부분의 변환
10진법 자릿수가 가지는 의미에서 봤듯이 2진수도 같은 원리이다. 위 자료처럼 2진수의 정수 부분이 1111이라 생각해보자.
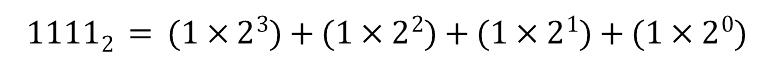
(10진법에서 1을 나타내는)1은 2로 1번 나누었을 때의 나머지이다.
(10진법에서 2를 나타내는)1은 2로 2번 나누었을 때의 나머지이다.
(10진법에서 4를 나타내는)1은 2로 3번 나누었을 때의 나머지이다.
(10진법에서 8을 나타내는)1은 2로 4번 나누었을 때의 나머지이다.
10진법에서 해석한 진법 시스템 방법으로 똑같이 2진법에서 해석을 해보았다. 그럼 다음과 같이 해석할 수 있다.

앞에 설명한 진법 원리를 이해한다면 이해할 수 있을 것이다. 이와 같은 원리로 2로 계속 나누어가면서 나머지를 역순으로 나열하면 된다. 8진법, 16진법 또한 같은 방법으로 변환할 수 있다.
#소수 부분의 변환
소수 부분의 변환 같은 경우는 2를 계속적으로 곱해가면서 정수 자리로 자리올림이 발생하는지를 보면 된다.
예를 들어 설명하겠다. 10진법 0.2를 2진법으로 변환해보겠다.

소수 부분을 2진법으로 표현하게 되면 무한소수가 된다. 따라서 유한한 비트를 사용하는 컴퓨터는 엄밀히 말하면 정확히 소수 부분을 표현할 수 없다. 대략적으로만 표현하는 것이다.
#총 정리 + 기타 진법 변환
- 10진법 -> 2진법: 정수 부분, 소수 부분 각각 2진수 변환 후 가운데 소수점 찍기
- 10진법 -> 8진법: 2진법으로 표현했던 방식과 동일하게 8로 나누어가며 나머지를 역순으로 나열
- 10진법 -> 16진법: 동일한 방법으로 16으로 나누어가며 나머지를 역순으로 나열(16진법은 나머지를 10 이상부터 알파벳으로 표현)
- 2진법 -> 10진법: 각 자리 지수승에 맞춰 더해주기
- 2진법 -> 8진법: 정수 부분은 소수점 기준 왼쪽 방향으로 3자리씩, 소수 부분은 소수점 기준 오른쪽 방향으로 3자리씩 변환
- 2진법 -> 8진법: 정수 부분은 소수점 기준 왼쪽 방향으로 4자리씩, 소수 부분은 소수점 기준 오른쪽 방향으로 4자리씩 변환
- 8진법 -> 2진법: 8진법 1자리당 2진법 3비트 변환
- 16진법 -> 2진법: 16진법 1자리당 2진법 4비트 변환
